Analysis/Topology: Bounded and Totally Bounded Sets

Definitions

Bounded set: Let <M,ρ> be a metric space. We say that the subset A of M is bounded if there exists a positive number L such that ρ(x,y)≤L (x,y∈A) (Wikipedia)
Diameter of a set: If A is bounded, we define diameter of A (denoted by diam A) as diam A= ${l.u.b.}_(x,y\in A)$ ρ(x,y). If A is not bounded we write diam A=∞. (Wikipedia)
Totally bounded sets: Let <M,ρ> be a metric space. The subset A of M is said to be totally bounded if given ϵ>0, there exist a finite number of subsets $A_1 , A_2 , ..., A_n$ of M such that diam $A_k$ < ϵ (k=1,2,…,n) and such that $A\subset \cup_{k=1}^n A_k$ . (Wikipedia)
Cover of a set: If for a set A, if it is a subset of union of sets $A_1,A_2,...$ then we say $A_k$ cover A. (Wikipedia)
Totally bounded sets: A⊂M is totally bounded iff for every ϵ>0, A can be covered by a finite number of subsets of M whose diameters are all less than ϵ.
ϵ-dense: Let A be a subset of the metric space M. The subset B of A is said to be ϵ-dense in A (where ϵ>0) if for every x∈A there exists y∈B such that ρ(x,y)<ϵ. That is, B is ϵ-dense in A if each point of A is within distance ϵ from some point of B.

Theorems

If the subset A of the metric space <M, ρ> is totally bounded, then A is bounded.
The subset A of the metric space <M, ρ> is totally bounded if and only if for every ϵ>0, A contains a finite subset { $x_1,x_2,…,x_n$ } which is ϵ-dense in A.
Let <M,ρ> be a metric space. The subset A of M is totally bounded if and only if every sequence of points of A contains a Cauchy subsequence.
A subset of $\mathbb R^2$ is bounded iff it is contained in a square of finite side length.
A subset of $\mathbb R^3$ is bounded iff is contained in a cube of finite side length.
In $\mathbb R$ a set is totally bounded if and only if it is bounded. Hence, any bounded subset of $\mathbb R$ is an example of totally bounded subset of $\mathbb R$
$\mathbb R^n$ is totally bounded if and only if it is bounded A subset A of $\mathbb R_d$ is totally bounded if and only if A contains only finite number of points.

Examples and Counterexamples

In $\mathbb R$ , [0,∞) is not bounded. But in $\mathbb R_d$ , ρ(x,y)≤1,∀x,y∈[0,∞) and hence it is bounded. (L=1). Hence, all subsets of $latex \mathbb R_d$ are bounded.
In $\mathscr{l}^2$ , let $e_k$ be the sequence whose all terms are 0 except kth term. Consider the set $E= \cup_{n=1}^\infty {e_k }$ . Then E is bounded with diameter √2

This set is not bounded in R^2. (Blue shaded area)

Bounded and totally bounded: [0,2] in R
- $\{<x,y>\in\mathbb R^2 |x^2+y^2=9\}$ (circle with radius 3, centred at origin)
- $\{<x,y,z>\in \mathbb R^3 |x^2+y^2+z^2=4\}$ (sphere with radius 2, centred at origin)
- Finite sets in $\mathbb R_d$
Bounded but not totally bounded: Interval [0,2] in $\mathbb R_d$

Quizzes

1. Which of the following set is totally bounded in 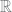$\mathbb{R}$

[0,∞)

A set is bounded iff it is totally bounded in 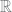$\mathbb{R}$

[0,1)

(-∞, 2)

A set is bounded iff it is totally bounded in 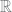$\mathbb{R}$

All of the above

A set is bounded iff it is totally bounded in 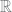$\mathbb{R}$ . [0,1) is the only bounded set in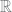 $\mathbb{R}$

Let M be a metric space. Which of the following is true?

A totally bounded set in a metric space need not be bounded.

A set is totally bounded then it is bounded.

A bounded set in a metric space need not be totally bounded.

Interval [0,2] in $\mathbb R_d$

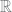If M = $\mathbb{R}$ , then every set is bounded and totally bounded.

(-∞, 2) is a subset of 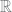$\mathbb{R}$ and is neither bounded nor totally bounded.

If M = $\mathbb{R}_d$ , then every set is bounded and totally bounded.

[0,2] in $\mathbb R_d$ is bounded but not totally bounded.

External Reading Materials

Bounded Sets on Wikipedia
Totally Bounded Sets on Wikipedia
Bounded Sets on WolframAlpha
Bounded Sets on LibreTexts
Bounded Sets on MathOnline
Which metric spaces are totally bounded? on Math.SE

This article was previously posted in my old blog – reposted here with additional insights.

One Comment Add yours

Pingback: Real Analysis: Bounded and Totally Bounded Sets | Lecture Diaries

Mathematicos

Analysis/Topology: Bounded and Totally Bounded Sets

Definitions

Theorems

Examples and Counterexamples

Quizzes

External Reading Materials

Published by jessepfrancis

One Comment Add yours

Leave a Reply Cancel reply

Definitions

Theorems

Examples and Counterexamples

Quizzes

External Reading Materials

Share this:

Like this:

Published by jessepfrancis

One Comment Add yours

Leave a Reply Cancel reply